[Optical Flow/05] Lucas-Kanade Algorithm, Part II
This post is written by YoungJ-Baek
You can see the original Korean version at Searching Fundamental
Preface
In the previous post, we looked at how to calculate optical flow using the assumptions added to the Lucas-Kanade algorithm. In this post, we will discuss methods to improve the accuracy of the Lucas-Kanade algorithm using weights and techniques proposed to handle big motions. Additionally, we will mention the inherent issues of sparse optical flow that were not covered in the previous post.
Weighted Window
The Lucas-Kanade Algorithm is designed based on a window. Pixels within the same window have the same Optical Flow value. Although it is an assumption, it is not questioned much. However, if we think a little more, it is not very realistic, especially at the edges where there can be significant errors. Weighted windows provide some correction to the Lucas-Kanade assumption to make it more practical. The closer to the center of the window, the larger the weight, and the pixels within the window can have different values. Gaussian weights are commonly used.
\[A^{T}WAv=A^TWb \quad \Rightarrow \quad v=(A^TWA)^{-1}A^TWb\] \[\begin{bmatrix} V_x \\V_y \end{bmatrix}=\begin{bmatrix} \sum _iw_iI_x(q_i)^2&\sum _iw_iI_x(q_i)I_y(q_i) \\ \sum _iw_iI_y(q_i)I_x(q_i)& \sum _iw_iIy(q_i)^2 \\ \end{bmatrix}^{-1}\begin{bmatrix} -\sum _iw_iI_x(q_i)I_t(q_i) \\ -\sum _iw_iI_y(q_i)I_t(q_i) \end{bmatrix}\]The above equation is the result of adding weight to the conventional Lucas-Kanade expansion. The equation using Gaussian weight uses the Gaussian function value of the distance between the i-th $p$ and $q$ values to determine the i-th $w$ value.
Coarse to Fine Strategy (Image Pyramid)
As mentioned in the previous post, the Lucas-Kanade Algorithm is vulnerable to big motion (large displacement). Why is that? Do you remember that Short Displacement was assumed for Taylor Approximation? It would be a natural answer. However, if we leave it vulnerable to big motion, it would be difficult to use in the real world. Therefore, a little trick is applied. In traditional image processing, it is called the Image Pyramid technique, while in recent computer vision fields using deep learning, it is called the Coarse to Fine Strategy.
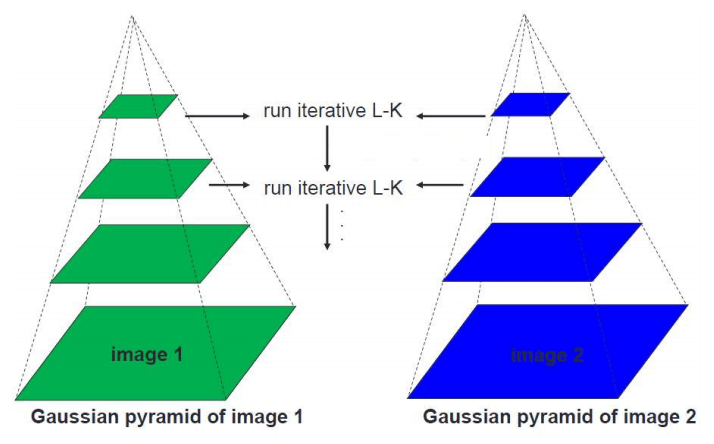Image Pyramid of Lucas-Kanade Algorithm
Image Pyramid (Coarse to Fine Strategy) is a technique that transforms an image from a low-resolution (down-scaled) to a high-resolution (up-scaled) image, widening the convergence of algorithms that operate on the entire image domain. By utilizing this technique, large displacements in reality can appear as short displacements. Even if there are movements of more than 50 pixels in the original image, they can be minimized to within 5 pixels by down-scaling.
This method measures short displacements in the down-scaled image and obtains the final flow map by up-scaling to the original image. However, this method has the problem of error propagation because a lot of information is lost during the down-scaling process, and errors generated in the low-resolution image are not corrected but instead maintained during the up-scaling process.
Error Propagation
Leave a comment